A/B Test란?
1. A/B Test란?
A/B Test는 특정 처치(treatment)가 효과가 있는지 알아내는 방법입니다. 여기서 treatment는 실험에 따라 새로운 회원가입 방식/프로모션 등이 될 수 있습니다.
이를 위해, 집단을 임의로 두 집단으로 나누고(treatment/control group), 특정 그룹에만 treatment를 적용합니다.
이후 두 집단의 성과를 비교함으로써 treatment의 효과를 측정합니다.
여기서 핵심은 두 집단이 랜덤하게 분배되어야 한다는 것입니다.
즉, 두 그룹은 treatment를 제외한 모든 특성이 동일하여야 합니다.
그렇지 않으면, selection bias로 인하여 treatment의 효과가 잘못 측정될 수 있습니다.
2. 테스트 결과 검증
실험 결과, treatment group이 control group보다 성과지표가 높다면 실제로 해당 treatment는 효과가 있다고 볼 수 있을까요?
그럴 수도 있지만 아닐 수도 있습니다.
예를 들어, 광고 크기를 키우는 것이 클릭률을 높이는데 도움이 되는지 테스트한다고 가정해봅시다.
B group만 광고 크기를 조금 키웠고, 다음과 같은 실험 결과를 얻었습니다
| 구분 | A group (Control group) | B group (Treatment group) |
| 노출수 | 1000번 | 1100번 |
| 클릭수 | 20번 | 30번 |
| 클릭률 | 0.02 | 0.027 |
얼핏 보면, 광고 크기를 키우는 것이 클릭률을 +0.7%p 증가시키는 효과가 있는 것 같지만
실제 가설 검정을 해보면 이는 유효하다고 볼 수 없습니다.
가설 검정 과정은 아래와 같습니다.
- 분포: 이항분포 (클릭 여부이기 때문)
- 귀무가설: P(A)-P(B)=0
- 대립가설: P(A)-P(B)<0
n이 충분히 커, 표본비율의 차는 정규분포를 따릅니다. (보통 n>=30이면 정규분포를 따름)
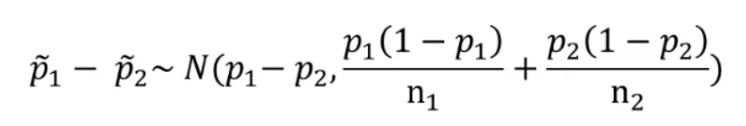
표준화를 진행하고 P(A)-P(B)=0으로 가정했기 때문에 합동 표준 비율을 이용하면 최종 검정 통계량은 다음과 같습니다

Z-test statistic: -1.0918
P-value: 0.1375(이를 파이썬 코드로 구현한 것은 GitHub을 참고해주세요.)
p-value가 0.1375로 유의수준 0.05 (보통 5%를 잡는다)보다 크기 때문에 효과가 있다고 보기 어렵습니다. (단순 표본오차)
이처럼 단순 표본오차를 효과로 오인할 수 있으니, 실험 결과를 얻었다면 그 것이 유의미한지 검증하여야 합니다.