Introduction

tabular data 학습에 최적인 deep neural network 모델
- neural network 구조를 decision-tree와 같이 만들어서 사용

neural network가 tree-based 모델보다 나은점
- 성능 향상
- end-to-end 방법 사용 가능
- tabular 형태 외에 다른 데이터(이미지/텍스트)와 결합 가능
- streaming data에도 사용 가능(tree-based model은 global data가 아닌 streaming data를 사용하면 성능이 하락함)
- semi-supervised learning을 사용할 수 있음

Tabnet 특징

: the soft feature selection ability into a sequential attention-based network architecture, with controllable sparsity

end-to-end learning
- 다른 tabular data 기법과 달리 end-to-end learning을 활용하여 다른 피쳐 전처리가 필요하지 않음
- conventional gradient descent-based optimization을 활용하여 훈련됨

sequential attention mechanism
- 각 decision step에서 sequential attention mechanism을 활용하여 더 효율적인 학습과 해석이 가능해짐
- 인스턴스별로 설계하여 인스턴스별로 어떤 피쳐에 집중할지 결정할 수 있음

성능과 해석 가능성 둘 다 가능 (soft feature selection을 통해)
- 단일 모델에서 feature selection과 output mapping을 모두 수행
  - 다른 tabular data learning model에 비해 성능이 높음
  - local interporetability 와 global interpretability 모두 가능

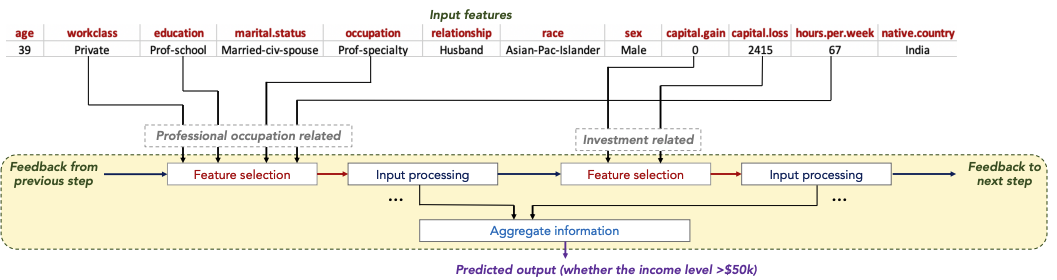
TabNet Model

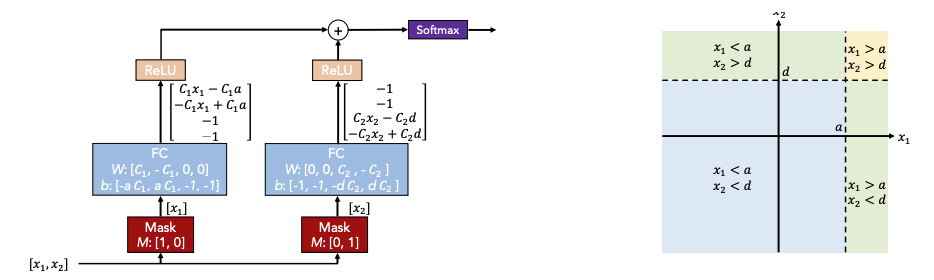
Principles

conventional neural network를 이용하여 decision tree 같이 학습을 진행
1. masking을 통해 관련있는 feature를 선택
1. 선형변환 및 bias(경계를 나타냄)를 더함
1. 각 region에 대해 ReLU 적용 후 더함
1. 최종적으로 softmax

Overall Architecture

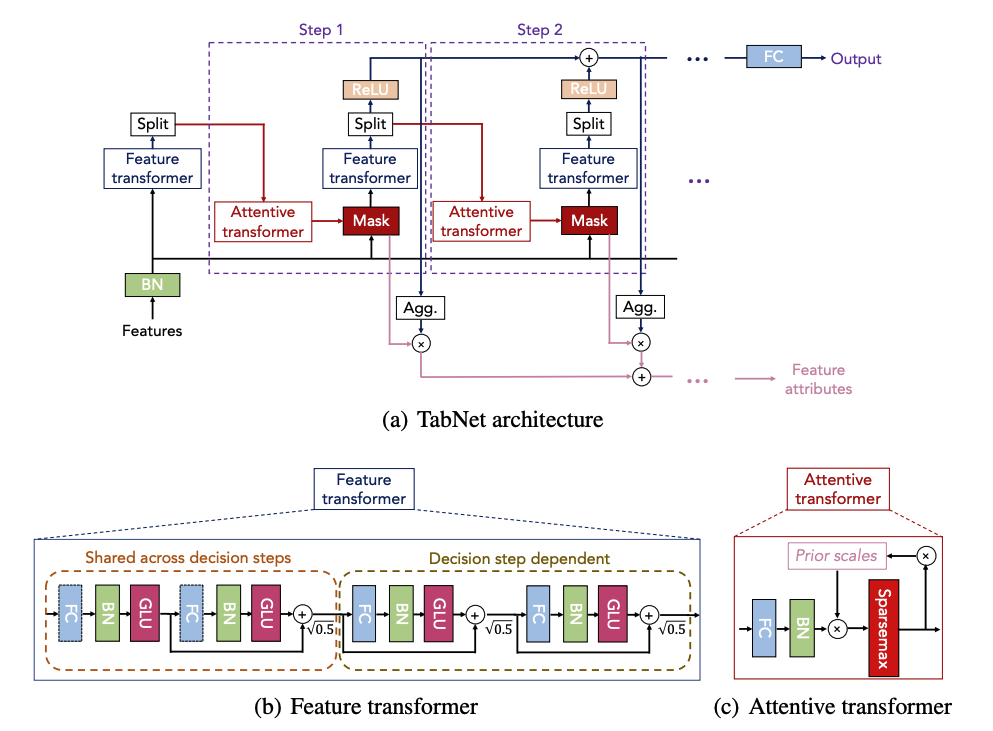
(a) TabNet is based on sequential multi-step processing, with Nsteps decision steps

각 decision step은 feature transformer, attentive transformer, feature masking으로 구성되어 있음

각 decision step은 두가지 input을 받음
1. 공통적인 $\in R^{BXD}$
1. $i-1)^{th}$ 에서 처리된 정보

각 decision step은 두가지 output을 산출
1. 다음 step에서 사용할 정보(attentive transformer의 input)
1. global output을 위한 정보

mask 는 feature import 에 대한 인사이트를 제공

(b)

4개의 layer가 존재

두개는 모든 decision step에 공유되고 나머지 2개는 결정 step에 따라 다름

(c)

prior scale: 현재의 decision step 이전에 각 feature가 얼마나 사용되었는지를 나타내는 정보를 담고 있음

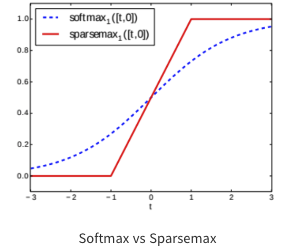
sparsemax: 중요한 feature는 1, 아닌 것은 0으로 mask를 만들어줌 (softmax보다 희소한 결과값을 만듦)
- feature 개수가 증가할수록 0,1 사이의 기울기를 가지는 구간이 적어지고 1이 되는 구간은 극소화됨

Data preprocessing

categorical feature는 학습가능한 임베딩으로 매핑

global noramlization은 사용하지 않고, batch noramlization만 사용

Feature selection

[Mask]

mask $M[i]∈RBXDM[i]\in R^{BXD}$ 를 통해 soft selection을 함. sparsemax 함수를 활용하기 때문에 마스크 벡터의 총합은 1 ( $∑j=1DM[i]b,j=1\sum_{j=1}^{D}{M[i]_{b,j}}=1$ )
- 전단계로부터 처리된 attentive transform( $a [i - 1]$ )를 사용하는데, 이를 얼마나 선택할지 $P [i - 1]$ 로 조절하여 mask를 최종적으로 계산
- $h_{i}$ 는 FC layer를 사용하여 학습 가능한 변수

$M[i] = sparsemax(P[i-1]·h_{i}(a[i-1]))$
- $\,scale\,term$
- $h_{i}=hidden\,layer$
- $blocka=attentive\,\,transformer\,\,block$
- $stepi=decision\,step$

[Prior scale term]

$P [i]$ 는 prior scale term으로 이전에 피쳐가 얼마나 사용되었는지를 나타냄 (한 피쳐가 지나치게 중복선택되는 것을 방지)
- $P[i]=Πj=1i(γ−M[j])P[i]=\Pi_{j=1}^{i}{(\gamma-M[j]})$
  - $parameter\gamma= relaxation\,\,parameter$
  - 1이면 하나의 decision step에서 사용, 값이 증가할 수록 여러개의 decision model에서 사용될 수 있도록 유연성을 제공

P[i]=Πj=1i(γ−M[j])P[i]=\Pi_{j=1}^{i}{(\gamma-M[j]})

Feature processing

Feature transform는 4개의 블럭으로 구성되어 있음
- 앞의 2개 블럭은 전체 decision step에서 가중치를 공유
- 각 블럭은 활성함수로 GLU를 적용하고, $0.5\sqrt{0.5}$ 로 정규화된 skip connection을 적용
- 빠른 학습을 위해 큰 배치 사이즈를 선택하고 Ghost Batch Normalization을 적용

feature transform은 두 가지 output을 산출
- $f_{i}(M[i]f)=[d[i],a[i]]$
1. $d [i]$ : decision step output(global output 계산을 위한 input)
1. $a [i]$ : 다음 decision step을 위한 input (attentive transformer의 input)

Overall decision embedding $d_{out}$ 과 예측값 $y^\hat{y}$
- $dout=∑i=1NstepsReLU(d[i])d_{out}=\sum_{i=1}^{N_{steps}}ReLU(d[i])$
- $y^=Wfinaldout\hat{y}=W_{final}d_{out}$
  - $W_{final}:linear\,mapping\,layer$

Interpretability

feature selection mask를 통해 feature importance에 관한 인사이트를 얻을 수 있음

$Magg−b,j=∑i=1Nstepsηb[i]Mb,j[i]/∑j=1D∑i=1Nstepsηb[i]Mb,j[i]M_{agg-b,j}=\sum_{i=1}^{N_{steps}}{\eta}_{b}[i]M_{b,j}[i]/\sum_{j=1}^{D}\sum_{i=1}^{N_{steps}}{\eta_{b}[i]M_{b,j}[i]}$
- $M_{b,j}[i]$ : i번째 decision step에서의 b샘플에 대한 j번째 Feature의 importance
- $ηb[i]\eta_{b}[i]$ : i번째 decision step의 output에 대한 importance ( $M_{b,j}[i]$ 의 weight로 사용할 수 있음)
- 정규화는 각 feature importance의 합을 1로 만들기 위해 사용됨 ( $∑j=1DMagg−b,j=1\sum_{j=1}^{D}M_{agg-b,j}=1$ )

데이터 분석가의 공부노트

[논문 리뷰] TabNet: Attentive Interpretable Tabular Learning